Choose the correct servo motion control algorithms for your application
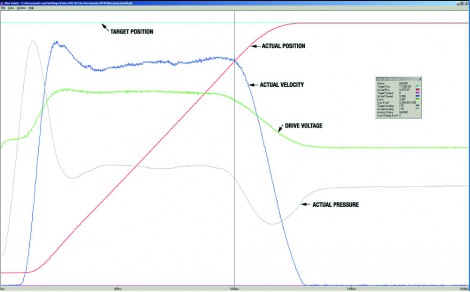
The derivative gain (D) provides electronic damping that helps to keep the actuator from oscillating as the proportional gain is increased. Ideally, increasing the derivative gain will tend to dampen or even eliminate the oscillations. How well the derivative gains work depends on a few important factors, like feedback resolution and maintaining known sampling times. Since the derivative gain is multiplied by the error in velocity, it is important to be able to measure and calculate velocities accurately.
Although the three gains of the PID seem to be independent of each the other, there are mathematical relationships between the PID gains that must be maintained to achieve a critically-damped or over-damped response that doesn't overshoot the set point.
Feed forwards are the key to good motion profile tracking
As described above, using the P, I, and D gains together in the control algorithm are helpful in improving the response of the system. However, a limitation to using PID-based controls alone is that there won't be any output generated to drive the valve unless there is an error. In many applications this is not a problem, but precise tracking actually requires estimating the required output before the error occurs. That's where feed forward gains play a role. Unlike PID gains, which are multiplied by the feedback error, feed forward gains are predictive gains that are multiplied by the target velocity and acceleration and summed together to generate a contribution to the output.
The concept is really very simple. In precisely tuned hydraulic systems, separate gains are required to achieve the desired velocity and acceleration in each direction of motion. As the motion controller moves the target position from one point to another, it also generates a target velocity and acceleration.
These values are then multiplied by their respective feed forward gains to generate the required move output at the current velocity and acceleration. In theory, if the predictive gains are computed correctly, there should be no error. But real-world systems are seldom exactly linear and the loads on many systems change from cycle to cycle. This causes errors that the PID can correct. In general, one should be able to predict the required output within 5% of the desired goal using feed forwards, so the PID component of the closed-loop control algorithm only needs to correct the last 5%. This is much better than forcing the PID gains to do all the work.
Since the controller multiplies the instantaneous velocity and acceleration by the feed forward gains to determine the feed forward contribution to the output, these values should change smoothly without discontinuity or the control output will also change in steps.
Ideally, motion profiles with simple linear ramps (trapezoidal moves - see Figure 1a) should only use velocity feed forwards, since there are step changes in acceleration. Step changes in the acceleration feed forward will cause step changes in the output, which can excite higher frequencies in the system, resulting in oscillation and following errors. (Physical systems cannot make step changes in acceleration anyway and attempts to do so will cause following errors which may or may not be tolerable). In order to use acceleration feed forwards to the best advantage, S-curves or some other acceleration limiting technique must be used (Figure 1b). Feed forwards should be used whenever axes must be tightly synchronised, or when precise gearing or profile tracking is needed, including applications such as flying cutoff saws and flying shears.
-
PPMA 2025
23 September, 2025, 9:30 - 25 September, 2025, 16:00
NEC, Birmingham UK -
Advanced Engineering Show 2025
29 October, 2025, 9:00 - 30 October, 2025, 16:00
NEC, Birmingham UK










