Choose the correct servo motion control algorithms for your application

07 June, 2019

There are thousands of different hydraulic motion control applications, and designers must choose the optimum control algorithm to get the best performance out of each application. Sometimes a combination of control methods is required. This article describes some of the more common algorithms that are supported by commercially-available hydraulic motion controllers. The article will focus on hydraulic positioning, and just touch on pneumatic and pressure control.

Open-loop control

A surprising number of applications use open-loop control. These include cases where the actuator must move to unknown hard stop positions in order to align or measure objects such as logs in a sawmill. In such applications, where position and velocity control are not critical, open-loop control is often preferred over closed-loop control. With open-loop control, the motion controller is not working actively to match the actual position, velocity, or pressure to computed target values; hence it does not track the error between the actual and target values. Since there is no build up in error, the actuator will not move abruptly forward should the load be reduced suddenly. Open loop control is often combined with closed-loop control with each used in different parts of the machine cycle where it is best suited. For example, open-loop can be used in the retract direction to quickly open a press so a part can be ejected. Tuning is simplified since only the extend (pressing) direction must be tuned - the open loop part does not.

Closed-loop control

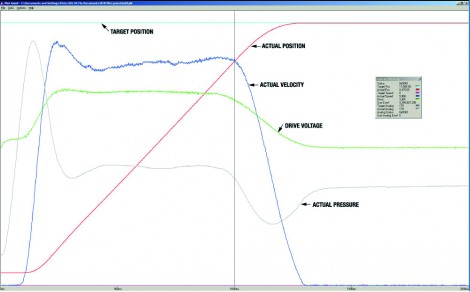
Applications requiring profile following, synchronisation, gearing, or a high degree of flexibility, accuracy and speed, or those needing the ability to maintain precision with changing loads, must use closed-loop control that comes in many flavours. Some simple analogue controllers operate with just proportional control, where the drive sign is a function of the magnitude of the difference between actual and target position or pressure.

Proportional control (P) by itself will work adequately on some hydraulic systems providing there is enough mechanical friction to provide damping. However, many hydraulic systems tend to be under-damped (like a mass on a spring) so adding only P gain tends to make any oscillations worse. And since a P-gain-only controller must have error to get the required output to move at the desired speed, there is a lot of following error and the following error increases as velocities increase. For tighter closed-loop control, other gain terms are required, and each plays a different part.

The integrator gain (I) is often necessary to get the axis to move into position quickly and reliably. As pointed out above, a proportional-only control system needs to have an error in order to generate a non-zero output. In an ideal world, even a little output would move the actuator to its set point, but the mechanical realities of a system, such as changes in the null characteristics of a valve, or friction between the moving parts, may keep the actuator from getting to the target set point. The integrator gain component of the control equation integrates error over time, eventually causing the output to increase or 'wind up' to whatever value is necessary to cause the actuator to move.